코드트리 | 코딩테스트 준비를 위한 알고리즘 정석
국가대표가 만든 코딩 공부의 가이드북 코딩 왕초보부터 꿈의 직장 코테 합격까지, 국가대표가 엄선한 커리큘럼으로 준비해보세요.
www.codetree.ai
문제
격자가 있고, 모든 위치에는 포탑이 존재합니다. (즉, 포탑의 개수는 개)
각 포탑에는 공격력이 존재하며, 상황에 따라 공격력이 줄어들거나 늘어날 수 있습니다. 또한, 공격력이 이하가 된다면, 해당 포탑은 부서지며 더 이상의 공격을 할 수 없습니다. 최초에 공격력이 인 포탑 즉, 부서진 포탑이 존재할 수 있습니다.
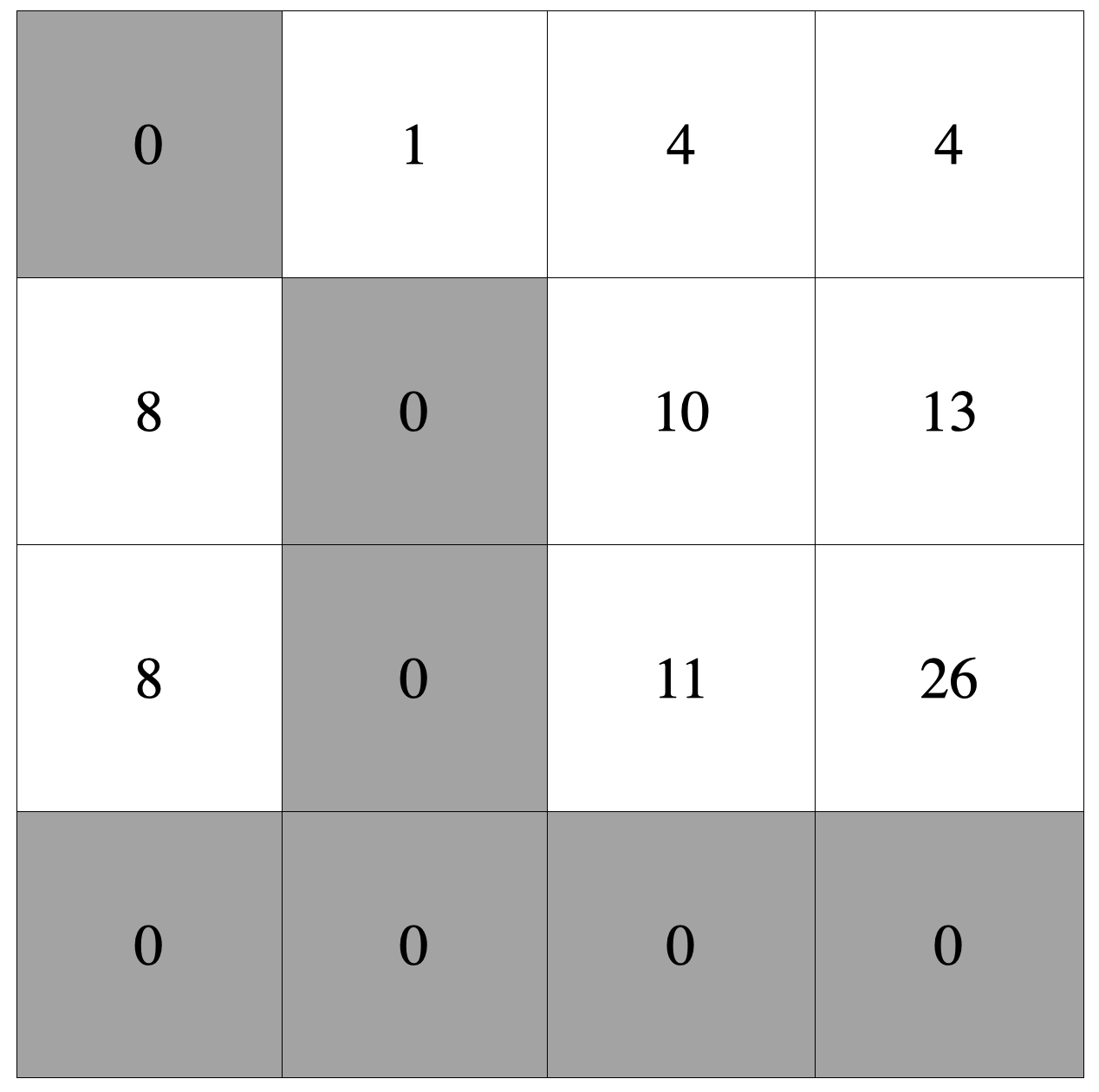
아래와 같은 크기의 격자를 생각해보겠습니다. , , 를 포함한 총 개의 칸은 이미 부서진 포탑을 의미합니다.
하나의 턴은 다음의 4가지 액션을 순서대로 수행하며, 총 번 반복됩니다.
만약 부서지지 않은 포탑이 개가 된다면 그 즉시 중지됩니다.
1. 공격자 선정
부서지지 않은 포탑 중 가장 약한 포탑이 공격자로 선정됩니다. 공격자로 선정되면 가장 약한 포탑이므로, 핸디캡이 적용되어 만큼의 공격력이 증가됩니다.
가장 약한 포탑은 다음의 기준으로 선정됩니다.
- 공격력이 가장 낮은 포탑이 가장 약한 포탑입니다.
- 만약 공격력이 가장 낮은 포탑이 2개 이상이라면, 가장 최근에 공격한 포탑이 가장 약한 포탑입니다. (모든 포탑은 시점 에 모두 공격한 경험이 있다고 가정하겠습니다.)
- 만약 그러한 포탑이 2개 이상이라면, 각 포탑 위치의 행과 열의 합이 가장 큰 포탑이 가장 약한 포탑입니다.
- 만약 그러한 포탑이 2개 이상이라면, 각 포탑 위치의 열 값이 가장 큰 포탑이 가장 약한 포탑입니다.
위의 예시에서 공격자를 선정해보면, 가장 낮은 공격력은 이기 때문에, 아래 그림과 같이 위치에 있는 포탑이 공격자로 선정되며, 공격력이 만큼 증가하여 가 됩니다.

2. 공격자의 공격
위에서 선정된 공격자는 자신을 제외한 가장 강한 포탑을 공격합니다.
가장 강한 포탑은 위에서 정한 가장 약한 포탑 선정 기준의 반대이며, 다음과 같습니다.
- 공격력이 가장 높은 포탑이 가장 강한 포탑입니다.
- 만약 공격력이 가장 높은 포탑이 2개 이상이라면, 공격한지 가장 오래된 포탑이 가장 강한 포탑입니다. (모든 포탑은 시점 에 모두 공격한 경험이 있다고 가정하겠습니다.)
- 만약 그러한 포탑이 2개 이상이라면, 각 포탑 위치의 행과 열의 합이 가장 작은 포탑이 가장 강한 포탑입니다.
- 만약 그러한 포탑이 2개 이상이라면, 각 포탑 위치의 열 값이 가장 작은 포탑이 가장 강한 포탑입니다.
위의 예시에서 공격 대상자를 선정해보겠습니다. 공격 대상인 가장 강한 포탑은 공격력이 가장 큰 의 공격력을 가진 위치의 포탑이 됩니다.

공격을 할 때에는 레이저 공격을 먼저 시도하고, 만약 그게 안 된다면 포탄 공격을 합니다. 각 공격의 규칙은 다음과 같습니다.
(1) 레이저 공격
레이저는 다음의 규칙으로 움직입니다.
- 상하좌우의 4개의 방향으로 움직일 수 있습니다.
- 부서진 포탑이 있는 위치는 지날 수 없습니다.
- 가장자리에서 막힌 방향으로 진행하고자 한다면, 반대편으로 나옵니다. (예를 들어, 위의 예시에서 에서 오른쪽으로 두번 이동한다면, -> -> 순으로 이동합니다.)
레이저 공격은 공격자의 위치에서 공격 대상 포탑까지의 최단 경로로 공격합니다. 만약 그러한 경로가 존재하지 않는다면 (2) 포탄 공격을 진행합니다. 만약 경로의 길이가 똑같은 최단 경로가 2개 이상이라면, 우/하/좌/상의 우선순위대로 먼저 움직인 경로가 선택됩니다.
최단 경로가 정해졌으면, 공격 대상에는 공격자의 공격력 만큼의 피해를 입히며, 피해를 입은 포탑은 해당 수치만큼 공격력이 줄어듭니다. 또한 공격 대상을 제외한 레이저 경로에 있는 포탑도 공격을 받게 되는데, 이 포탑은 공격자 공격력의 절반 만큼의 공격을 받습니다. (절반이라 함은 공격력을 로 나눈 몫을 의미합니다.)
(2) 포탄 공격
공격 대상에 포탄을 던집니다. 공격 대상은 공격자 공격력 만큼의 피해를 받습니다. 추가적으로 주위 8개의 방향에 있는 포탑도 피해를 입는데, 공격자 공격력의 절반 만큼의 피해를 받습니다. (절반이라 함은 공격력을 로 나눈 몫을 의미합니다.) 공격자는 해당 공격에 영향을 받지 않습니다. 만약 가장자리에 포탄이 떨어졌다면, 위에서의 레이저 이동처럼 포탄의 추가 피해가 반대편 격자에 미치게 됩니다.
위의 예시에서 공격자가 공격 대상을 레이저로 공격하기 위한 최단 경로는 아래 그림과 같습니다. 최단 경로가 2개 이상 있지만, 오른쪽으로 먼저 움직이는 것이 우선 순위가 높기 때문에, 다음의 경로가 선택된 것입니다. 최단 경로가 정해졌기 때문에, 공격 대상에는 만큼의 피해를 입히고, 경로에 있는 포탑에는 만큼의 피해를 입힙니다.

3. 포탑 부서짐
공격을 받아 공격력이 이하가 된 포탑은 부서집니다.
4. 포탑 정비
공격이 끝났으면, 부서지지 않은 포탑 중 공격과 무관했던 포탑은 공격력이 씩 올라갑니다. 공격과 무관하다는 뜻은 공격자도 아니고, 공격에 피해를 입은 포탑도 아니라는 뜻입니다.
위의 예시에서 공격과 무관했던 다음 4개의 포탑은 정비를 받아 공격력이 씩 증가합니다. 이렇게 첫 번째 턴이 종료됩니다.

다음 두 번째 턴이 시작되면, 다시 공격자 선정이 시작됩니다.
첫 번째 규칙에 따라 가장 공격력이 작은 만큼의 공격력을 가진 , , , 위치의 포탑이 공격자 후보가 됩니다. 두 번째 규칙에 의해 가장 최근에 공격한 포탑인 포탑이 가장 약한 포탑이므로 공격자로 선정됩니다. 마찬가지로 핸디캡으로 만큼의 공격력을 얻습니다.

다음으로 공격 대상을 선택하면, 공격력이 가장 높은 가 선택됩니다. 공격자의 위치에서 공격 대상의 위치까지 이동하는 경로가 없기 때문에, 레이저 공격은 불가능하여 포탄 공격을 수행하게 됩니다. 포탄은 공격 대상인 위치에 떨어지며, 공격 대상은 만큼의 피해를 받고, 주변 8개의 방향에 있는 포탑은 만큼의 피해를 받습니다.

마지막으로 공격과 무관했던 포탑은 정비를 받아 만큼의 공격력을 얻지만, 위의 예시에서는 부서지지 않은 포탑 중 공격과 무관했던 포탑이 없으므로, 최종 모습은 다음과 같습니다.

전체 과정이 종료된 후 남아있는 포탑 중 가장 강한 포탑의 공격력을 출력하는 프로그램을 작성해보세요.
입력 형식
첫 번째 줄에 , , 가 공백을 사이에 두고 주어집니다.
두 번째 줄부터 개의 줄에 걸쳐서 격자에 대한 정보가 주어집니다. 단, 최초에 부서지지 않은 포탑은 최소 개 이상 존재합니다.
출력 형식
첫 번째 줄에 번의 턴이 종료된 후 남아있는 포탑 중 가장 강한 포탑의 공격력을 출력합니다.
문제 요약

풀이(DFS 활용) - 시간초과


Code(DFS 활용) - 시간초과
# 1. 공격자 선정 함수 정의
def attaker() :
# 1-1. 이중 for문을 통해 공격력이 낮은 포탑 리스트 구하기
potential1 = []
power = float("inf")
for i in range(n) :
for j in range(m) :
if graph[i][j] and graph[i][j] <= power :
# 공격력이 같을 경우
if power == graph[i][j] : potential1.append([i, j])
# 공격력이 더 낮을 경우
else :
potential1 = [[i, j]]
power = graph[i][j]
if len(potential1) == 1 : return potential1[0]
# 1-2. 공격 시점 딕셔너리를 활용해 가장 최근에 공격한 포탑 리스트 구하기
potential2 = []
p = -1
for x, y in potential1 :
if period[x, y] == p : potential2.append([x, y])
elif period[x, y] > p :
potential2 = [[x, y]]
p = period[x, y]
if len(potential2) == 1: return potential2[0]
# 1-3. 가장 최근에 공격한 포탑 리스트를 행과 열의 합의 내림차순 -> 열의 내림차순으로 정렬
return sorted(potential2, key = lambda x : [-(x[0] + x[1]), -x[1]])[0]
# 2. 타켓 선정 함수 정의
def target() :
# 2-1. 이중 for문을 통해 공격력이 높은 포탑 리스트 구하기
potential1 = []
power = -float("inf")
for i in range(n) :
for j in range(m) :
if graph[i][j] and graph[i][j] >= power and [i, j] != attacker_point:
# 공격력이 같을 경우
if power == graph[i][j] : potential1.append([i, j])
# 공격력이 더 낮을 경우
else :
potential1 = [[i, j]]
power = graph[i][j]
if len(potential1) == 1 : return potential1[0]
# 2-2. 공격 시점 딕셔너리를 활용해 가장 나중에 공격한 포탑 리스트 구하기
potential2 = []
p = float('inf')
for x, y in potential1 :
if period[x, y] == p : potential2.append([x, y])
elif period[x, y] < p :
potential2 = [[x, y]]
p = period[x, y]
if len(potential2) == 1: return potential2[0]
# 2-3. 가장 나중에 공격한 포탑 리스트를 행과 열의 합의 오름차순 -> 열의 오름차순으로 정렬
return sorted(potential2, key = lambda x : [(x[0] + x[1]), x[1]])[0]
# 3. 레이저 공격을 위한 범위 함수 정의
def range_laser(x, y, d) :
global min_d, return_array
# 3-1. 종료 조건
if d >= min_d : return
if [x, y] == target_point :
min_d = d
return_array = range_laser_array[1:].copy()
# 3-2.
for dir_x, dir_y in [(0, 1), (1, 0), (0, -1), (-1, 0)] :
nx, ny = (x + dir_x) % n, (y + dir_y) % m
# 다음 위치가 방문한 적이 없고 부서진 포탑이 아닐 경우
if [nx, ny] not in range_laser_array and graph[nx][ny] :
# 방문 처리
range_laser_array.append([nx, ny])
# 레이저 공격 함수 실행
range_laser(nx, ny, d + 1)
# 방문 해제
range_laser_array.pop()
# 4. 포탄 공격을 위한 범위 함수 정의
def range_shell(x, y) :
# 4-1. 반환용 리스트 생성
range_shell_array = []
# 4-2.
for dir_x, dir_y in [(-1, -1), (-1, 0), (-1, 1), (0, 1), (1, 1), (1, 0), (1, -1), (0, -1)] :
nx, ny = (x + dir_x) % n, (y + dir_y) % m
# 해당 위치가 부서진 포탑이 아니면서 공격 위치가 아닌 경우
if graph[nx][ny] and [nx, ny] != [attacker_point[0], attacker_point[1]] :
# 반환용 리스트에 인덱스 삽입
range_shell_array.append([nx, ny])
# 4-3. 목표 지점 삽입
range_shell_array.append([target_point[0], target_point[1]])
# 4-4. 리스트 반환
return range_shell_array
# 5. 공격 함수 정의
def attack() :
power = graph[attacker_point[0]][attacker_point[1]]
# 5-1.
for x, y in return_array :
# 타겟일 경우 공격력만큼 감소
if [x, y] == target_point :
graph[x][y] -= power if graph[x][y] - power > 0 else graph[x][y]
# 이외의 경우 공격력의 절반만큼 감소
else :
graph[x][y] -= power//2 if graph[x][y] - power//2 > 0 else graph[x][y]
# 6. 부서지지 않은 포탑 개수 체크 함수 정의
def check() :
cnt = 0
# 6-1. 부서지지 않은 포탑 개수 체크
for i in range(n) :
for j in range(m) :
if graph[i][j] : cnt += 1
# 6-2. 개수가 1개일 경우 True, 이외의 경우 False 반환
return True if cnt == 1 else False
# 7. 결과 출력 함수 정의
def return_ans() :
ans = -float('inf')
# 7-1. 최댓값 구하기
for i in range(n) :
for j in range(m) :
if graph[i][j] : ans = max(ans, graph[i][j])
# 7-2. 최댓값 반환
return ans
# 8. 포탑 정비 함수 정의
def recovery() :
for i in range(n) :
for j in range(m) :
if graph[i][j] and [i, j] not in return_array and [i, j] != attacker_point :
graph[i][j] += 1
n, m, k = map(int, input().split())
graph = [list(map(int, input().split())) for _ in range(n)]
period = dict()
time = 1
for i in range(n) :
for j in range(m) :
period[i, j] = 0
for _ in range(k) :
# 9-1. 공격자 선정
attacker_point = attaker()
# 9-2. 공격자로 선정될 경우 공격력 증가
graph[attacker_point[0]][attacker_point[1]] += n + m
# 9-3. 공격자의 공격 시점 변경
period[attacker_point[0], attacker_point[1]] = time
time += 1
# 9-4. 타겟 선정
target_point = target()
# 9-5. 레이저 공격을 통한 경로 리스트 반환
min_d = float('inf')
range_laser_array, return_array = [attacker_point], []
range_laser(attacker_point[0], attacker_point[1], 0)
# 9-6. 레이저 공격이 불가능할 경우 포탄 공격을 통한 경로 리스트 반환
if not return_array :
return_array = range_shell(target_point[0], target_point[1])
# 9-7. 공격
attack()
# 9-8. 남은 포탑 개수가 1개일 경우 출력 후 종료
if check() :
print(return_ans())
break
# 9-9. 포탑 정비
recovery()
# 10. k번의 공격이 끝난 경우 결과 출력
else :
print(return_ans())소요시간 -DFS 활용

풀이(BFS 활용)


Code(BFS 활용)
from collections import deque
# 1. 공격자 선정 함수 정의
def attaker() :
# 1-1. 이중 for문을 통해 공격력이 낮은 포탑 리스트 구하기
potential1 = []
power = float("inf")
for i in range(n) :
for j in range(m) :
if graph[i][j] and graph[i][j] <= power :
# 공격력이 같을 경우
if power == graph[i][j] : potential1.append([i, j])
# 공격력이 더 낮을 경우
else :
potential1 = [[i, j]]
power = graph[i][j]
if len(potential1) == 1 : return potential1[0]
# 1-2. 공격 시점 딕셔너리를 활용해 가장 최근에 공격한 포탑 리스트 구하기
potential2 = []
p = -1
for x, y in potential1 :
if period[x, y] == p : potential2.append([x, y])
elif period[x, y] > p :
potential2 = [[x, y]]
p = period[x, y]
if len(potential2) == 1: return potential2[0]
# 1-3. 가장 최근에 공격한 포탑 리스트를 행과 열의 합의 내림차순 -> 열의 내림차순으로 정렬
return sorted(potential2, key = lambda x : [-(x[0] + x[1]), -x[1]])[0]
# 2. 타켓 선정 함수 정의
def target() :
# 2-1. 이중 for문을 통해 공격력이 높은 포탑 리스트 구하기
potential1 = []
power = -float("inf")
for i in range(n) :
for j in range(m) :
if graph[i][j] and graph[i][j] >= power and [i, j] != attacker_point:
# 공격력이 같을 경우
if power == graph[i][j] : potential1.append([i, j])
# 공격력이 더 낮을 경우
else :
potential1 = [[i, j]]
power = graph[i][j]
if len(potential1) == 1 : return potential1[0]
# 2-2. 공격 시점 딕셔너리를 활용해 가장 나중에 공격한 포탑 리스트 구하기
potential2 = []
p = float('inf')
for x, y in potential1 :
if period[x, y] == p : potential2.append([x, y])
elif period[x, y] < p :
potential2 = [[x, y]]
p = period[x, y]
if len(potential2) == 1: return potential2[0]
# 2-3. 가장 나중에 공격한 포탑 리스트를 행과 열의 합의 오름차순 -> 열의 오름차순으로 정렬
return sorted(potential2, key = lambda x : [(x[0] + x[1]), x[1]])[0]
# 3. 레이저 공격을 위한 범위 함수 정의
def range_laser(x, y, d) :
range_laser_array = []
# 3-1. 역추적을 위한 배열 생성
back_x = [[0 for _ in range(m)] for _ in range(n)]
back_y = [[0 for _ in range(m)] for _ in range(n)]
# 3-2. 방문 여부 리스트 생성 후 공격자 위치 방문 처리
visited = [[False for _ in range(m)] for _ in range(n)]
visited[x][y] = True
# 3-3. 큐에 공격자 위치 삽입
queue = deque()
queue.append((x, y))
# 3-4.
while queue :
# 3-4-1. 위치 인덱스 반환
x, y = queue.popleft()
# 3-4-2. 타겟에 도달할 경우 경로 역추적 후 리스트 반환
if [x, y] == [target_point[0], target_point[1]] :
# 방어 포탑 인덱스 삽입
range_laser_array.append([x, y])
# 경로 역추적
cx, cy = back_x[x][y], back_y[x][y]
while not (cx == attacker_point[0] and cy == attacker_point[1]) :
range_laser_array.append([cx, cy])
cx, cy = back_x[cx][cy], back_y[cx][cy]
# 리스트 반환
return range_laser_array
# 3-4-3.
for dir_x, dir_y in [(0, 1), (1, 0), (0, -1), (-1, 0)] :
nx, ny = (x + dir_x) % n, (y + dir_y) % m
# 방문하지 않고 부서지지 않은 포탑인 경우
if not visited[nx][ny] and graph[nx][ny] :
# 방문 처리
visited[nx][ny] = True
# 역추적 배열에 정보 입력
back_x[nx][ny] = x
back_y[nx][ny] = y
# 큐에 다음 위치 삽입
queue.append((nx, ny))
# 3-5. 공격이 불가능한 경우 빈 리스트 반환
return range_laser_array
# 4. 포탄 공격을 위한 범위 함수 정의
def range_shell(x, y) :
# 4-1. 반환용 리스트 생성
range_shell_array = []
# 4-2.
for dir_x, dir_y in [(-1, -1), (-1, 0), (-1, 1), (0, 1), (1, 1), (1, 0), (1, -1), (0, -1)] :
nx, ny = (x + dir_x) % n, (y + dir_y) % m
# 해당 위치가 부서진 포탑이 아니면서 공격 위치가 아닌 경우
if graph[nx][ny] and [nx, ny] != [attacker_point[0], attacker_point[1]] :
# 반환용 리스트에 인덱스 삽입
range_shell_array.append([nx, ny])
# 4-3. 목표 지점 삽입
range_shell_array.append([target_point[0], target_point[1]])
# 4-4. 리스트 반환
return range_shell_array
# 5. 공격 함수 정의
def attack() :
power = graph[attacker_point[0]][attacker_point[1]]
# 5-1.
for x, y in return_array :
# 타겟일 경우 공격력만큼 감소
if [x, y] == target_point :
graph[x][y] -= power if graph[x][y] - power > 0 else graph[x][y]
# 이외의 경우 공격력의 절반만큼 감소
else :
graph[x][y] -= power//2 if graph[x][y] - power//2 > 0 else graph[x][y]
# 6. 부서지지 않은 포탑 개수 체크 함수 정의
def check() :
cnt = 0
# 6-1. 부서지지 않은 포탑 개수 체크
for i in range(n) :
for j in range(m) :
if graph[i][j] : cnt += 1
# 6-2. 개수가 1개일 경우 True, 이외의 경우 False 반환
return True if cnt == 1 else False
# 7. 결과 출력 함수 정의
def return_ans() :
ans = -float('inf')
# 7-1. 최댓값 구하기
for i in range(n) :
for j in range(m) :
if graph[i][j] : ans = max(ans, graph[i][j])
# 7-2. 최댓값 반환
return ans
# 8. 포탑 정비 함수 정의
def recovery() :
for i in range(n) :
for j in range(m) :
if graph[i][j] and [i, j] not in return_array and [i, j] != attacker_point :
graph[i][j] += 1
n, m, k = map(int, input().split())
graph = [list(map(int, input().split())) for _ in range(n)]
period = dict()
time = 1
for i in range(n) :
for j in range(m) :
period[i, j] = 0
for _ in range(k) :
# 9-1. 공격자 선정
attacker_point = attaker()
# 9-2. 공격자로 선정될 경우 공격력 증가
graph[attacker_point[0]][attacker_point[1]] += n + m
# 9-3. 공격자의 공격 시점 변경
period[attacker_point[0], attacker_point[1]] = time
time += 1
# 9-4. 타겟 선정
target_point = target()
# 9-5. 레이저 공격을 통한 경로 리스트 반환
min_d = float('inf')
return_array = []
return_array = range_laser(attacker_point[0], attacker_point[1], 0)
# 9-6. 레이저 공격이 불가능할 경우 포탄 공격을 통한 경로 리스트 반환
if not return_array :
return_array = range_shell(target_point[0], target_point[1])
# 9-7. 공격
attack()
# 9-8. 남은 포탑 개수가 1개일 경우 출력 후 종료
if check() :
print(return_ans())
break
# 9-9. 포탑 정비
recovery()
# 10. k번의 공격이 끝난 경우 결과 출력
else :
print(return_ans())소요시간 -BFS 활용
'Coding Test > Codetree' 카테고리의 다른 글
| [Python/Codetree] 싸움땅 (0) | 2023.10.14 |
|---|---|
| [Python/Codetree] 코드트리 빵 (0) | 2023.10.13 |
| [Python/Codetree] 돌아가는 팔각 의자 (0) | 2023.10.03 |
| [Python/Codetree] 토스트 계란틀 (1) | 2023.10.03 |
| [Python/Codetree] 병원 거리 최소화하기 (0) | 2023.09.30 |
