https://www.acmicpc.net/problem/2307
2307번: 도로검문
그림 1은 어떤 도시의 주요 지점과 그 지점들 간의 이동시간을 나타낸 그래프이다. 그래프의 노드는 주요 지점을 나타내고 두 지점을 연결한 도로(에지)에 표시된 수는 그 도로로 이동할 때 걸리
www.acmicpc.net
문제
그림 1은 어떤 도시의 주요 지점과 그 지점들 간의 이동시간을 나타낸 그래프이다. 그래프의 노드는 주요 지점을 나타내고 두 지점을 연결한 도로(에지)에 표시된 수는 그 도로로 이동할 때 걸리는 분 단위의 시간을 나타낸다. 두 지점 a와 b를 연결하는 도로는 도로(a,b)로 표시한다.

그림 1
예를 들어 도로(1,2)와 도로(2,3)를 통하여 지점1에서 지점3으로 갈 때 걸리는 시간은 3분이다. 도로는 모두 양방향이라고 가정하므로 도로(a,b)와 도로(b,a)를 지날 때 걸리는 시간은 항상 같다고 한다.
어떤 범죄용의자가 입력 데이터에 표시된 도시로 진입하여 이 도시를 가장 빠른 시간 내에 빠져나가고자 한다. 그런데 이 사실을 알고 있는 경찰이 어떤 하나의 도로(에지)를 선택하여 이 도로에서 검문을 하려고 한다. 따라서 용의자는 이 도로를 피해서 가장 빠르게 도시를 탈출하고자 한다. 이 경우 경찰이 검문을 위하여 선택하는 도로에 따라서 용의자의 가장 빠른 탈출시간은 검문이 없을 때에 비하여 더 늘어날 수 있다.
문제는 도로검문을 통하여 얻을 수 있는 탈출의 최대 지연시간을 계산하는 것이다. 추가설명은 다음과 같다.
- 두 개의 지점을 직접 연결하는 도로가 있는 경우, 그 도로는 유일하다.
- 도시의 지점(노드)은 1에서 N번까지 N개의 연속된 정수로 표시된다.
- 용의자가 도시에 진입하는 지점은 항상 1번이고 도시를 빠져 나가기 위하여 최종적으로 도달해야하는 지점은 항상 N번 지점이다.
- 용의자는 검문을 피해서 가장 빨리 도시를 빠져나가고자 하고, 경찰은 적절한 도로를 선택하여 이 용이자들의 탈출시간을 최대한 지연시키고자 한다.
- 각 도시 지점 간을 이동하는 시간은 항상 양의 정수이다.
입력 도시의 도로망에 따라서 경찰이 어떤 도로를 막으면 용의자는 도시를 탈출하지 못할 수도 있다. 이 경우 검문으로 인하여 지연시킬 수 있는 탈출시간은 무한대이다. 이 경우에는 -1을 출력해야 한다.
그림 1에서 볼 때 검문이 없을 경우 용의자가 도시를 탈출하는데 걸리는 시간은 4분이다. 만일 경찰이 도로(4,3)을 막으면 그 탈출시간을 지연시킬 수 없으므로 지연시간은 0이다. 만일 도로(2,3)을 막으면, 용의자들이 가장 빠르게 탈출할 수 있는 시간은 5분이므로 탈출지연시간은 1분이고, 도로(3,6)을 막으면 탈출지연시간은 2분이다.
여러분은 입력 데이터에 표시된 도로망을 읽고, 경찰이 한 도로를 막고 검문함으로써 지연시킬 수 있는 최대시간을 정수로 출력하여야한다. 만일 지연효과가 없으면 0을 출력해야하고, 도시를 빠져나가지 못하게 만들 수 있으면(지연시간이 무한대) -1을 출력해야 한다.
입력
첫 줄에는 지점의 수를 나타내는 정수 N(6 ≤ N ≤ 1000)과 도로의 수 M(6 ≤ M ≤ 5000)이 주어진다. 그 다음 이어 나오는 M개의 각 줄에는 도로(a, b)와 그 통과시간 t가 a b t 로 표시된다. 단 이 경우 a < b 이고 1 ≤ t ≤ 10000이다.
출력
경찰이 하나의 도로를 막음으로써 지연시킬 수 있는 최대 시간을 정수로 출력한다. (단, 그 지연시간이 무한대이면 -1을 출력해야 한다.)
풀이
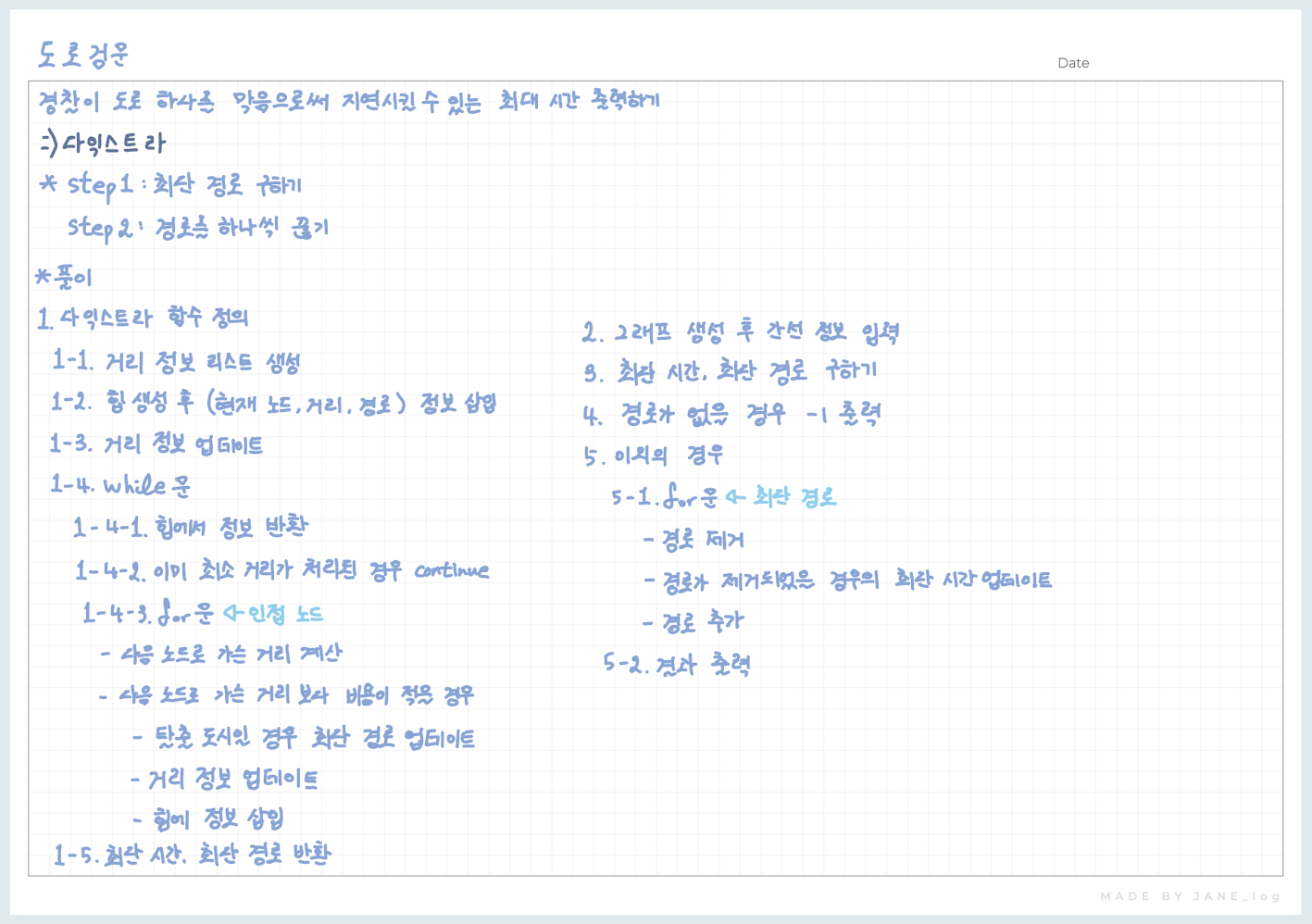
Code
import sys
from heapq import heappush, heappop
input = sys.stdin.readline
def solution(n, m):
# 1. 다익스트라 함수 정의
def dijkstra(start) :
min_route = []
# 1-1. 거리 정보 리스트 생성
distance = [float('inf') for _ in range(n+1)]
# 1-2. 힙 생성 후 (거리, 현재 노드, 경로) 정보 삽입
heap = []
heappush(heap, (0, start, [start]))
# 1-3. 거리 정보 업데이트
distance[start] = 0
# 1-4.
while heap :
# 1-4-1. 힙에서 정보 반환
d, now, route = heappop(heap)
# 1-4-2. 이미 최소 거리가 처리된 경우 continue
if distance[now] < d : continue
# 1-4-3.
for next, c in graph[now] :
# 다음 노드로 가는 비용 계산
next_d = d + c
# 다음 노드로 가는 거리보다 비용이 적을 경우
if distance[next] > next_d :
# 탈출 도시일 경우 최단 경로 업데이트
if next == n :
min_route = route + [next]
# 거리 정보 업데이트
distance[next] = next_d
# 힙에 정보 삽입
heappush(heap, (next_d, next, route + [next]))
# 1-5. 최단 시간, 최단 경로 반환
return distance[n], min_route
# 2. 그래프 생성 후 간선 정보 입력
graph = [[] for _ in range(n+1)]
for _ in range(m) :
a, b, t = map(int, input().split())
graph[a].append((b, t))
graph[b].append((a, t))
# 3. 최단 시간, 최단 경로 구하기
min_time, min_route = dijkstra(1)
# 4. 경로가 없을 경우 -1 출력
if not min_route : print(-1)
# 5. 이외의 경우
else :
update_max_time = -float('inf')
# 5-1.
for i in range(len(min_route) - 1) :
a, b = min_route[i], min_route[i+1]
# 경로 제거
for idx, info in enumerate(graph[a]) :
if info[0] == b :
info_a = info[:]
del graph[a][idx]
break
for idx, info in enumerate(graph[b]) :
if info[0] == a :
info_b = info[:]
del graph[b][idx]
break
# 경로가 제거되었을 경우의 최단 시간 업데이트
t, _ = dijkstra(1)
update_max_time = max(update_max_time, t)
# 경로 추가
graph[a].append(info_a)
graph[b].append(info_b)
# 5-2. 결과 출력
print(-1 if update_max_time == float('inf') else update_max_time - min_time)
if __name__ == "__main__" :
n, m = map(int, input().split())
solution(n, m)'Coding Test > Baekjoon' 카테고리의 다른 글
| [Python/BOJ] 10830. 행렬 제곱 (0) | 2023.12.13 |
|---|---|
| [Python/BOJ] 21275. 폰 호석만 (0) | 2023.12.13 |
| [Python/BOJ] 2533. 사회망 서비스(SNS) (0) | 2023.12.04 |
| [Python/BOJ] 15683. 감시 (0) | 2023.12.01 |
| [Python/BOJ] 1501. 영어 읽기 (0) | 2023.11.29 |
