독립 변수 데이터를 x, 숫자 0 초과인 경우에는 1, 이하인 경우에는 0을 부여한 레이블 데이터를 y라고 해 보자
Keras로 구현하는 로지스틱 회귀
이번 데이터는 앞서 배운 단순 선형 회귀 때와 마찬가지로 1개의 실수 x로부터 1개의 실수인 y를 예측하는 맵핑 관계를 가지므로 Dense의 output_dim, input_dim 인자값을 각각 1로 기재한다. 또한 시그모이드 함수를 사용할 것이므로 activation 인자값을 sigmoid로 기재해준다.
옵티마이저로는 가장 기본적인 경사 하강법인 sgd를 사용했다. 시그모이드 함수를 사용한 이진 분류 문제에 손실 함수로 크로스 엔트로피 함수를 사용할 경우 binary_crossentropy를 기재해주면 된다. 에포크는 200으로 한다.
x = np.array([-50, -40, -30, -20, -10, -5, 0, 5, 10, 20, 30, 40, 50])
y = np.array([0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1]) # 숫자 5부터 1from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras import optimizers
sgd = optimizers.SGD(lr = 0.01)
# 모델 선언
model = Sequential()
# 레이어 쌓기
model.add(Dense(1, input_dim = 1, activation = 'sigmoid'))
# 모델 컴파일
model.compile(optimizer = sgd, loss = 'binary_crossentropy', metrics = ['binary_accuracy'])
# 모델 요약
model.summary()
# 모델 훈련
model.fit(x, y, epochs = 200)총 200회에 걸쳐 전체 데이터에 대한 오차를 최소화하는 w와 b를 찾아내는 작업을 한다. 이후 실제값과 오차를 최소화하도록 값이 변경된 w와 b의 값을 가진 모델을 이용해 그래프를 그려보자.
import matplotlib.pyplot as plt
plt.plot(x, model.predict(x), 'b', x, y, 'k.')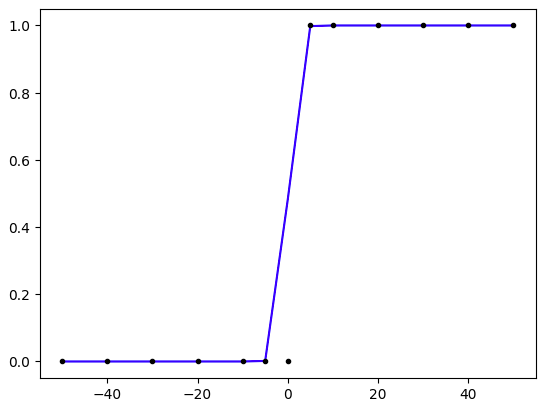
x의 값이 0일 때 y값이 0.5가 넘기 시작하는 것처럼 보인다. 이제 x의 값이 0보다 작은 값일 때의 x의 값과 0보다 클 때에 대해서 y값을 출력해보자.
print(model.predict([0, -1, -2, -3, -4.5]))
print(model.predict([1, 11, 21, 31, 500]))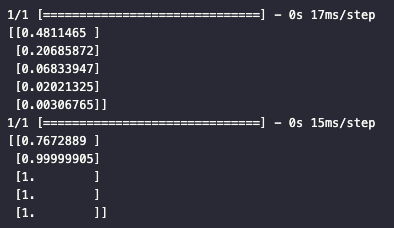
x의 값이 0보다 작을 때는 0.5보다 작은 값을, x의 값이 0보다 클 때는 0.5보다 큰 값을 출력하는 것을 볼 수 있다.
Pytorch로 구현하는 로지스틱 회귀
import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
x = torch.FloatTensor([[-50], [-40], [-30], [-20], [-10], [-5], [0], [5], [10], [20], [30], [40], [50]])
y = torch.FloatTensor([[0], [0], [0], [0], [0], [0], [0], [1], [1], [1], [1], [1], [1]]) # 숫자 0부터 1model = nn.Sequential(
nn.Linear(1, 1), # (input_dim, output_dim)
nn.Sigmoid()
)
# optimizer 설정
optimizer = optim.SGD(model.parameters(), lr = 0.01)
epochs = 200
for i in range(1, epochs+1) :
# H(x) 계산
hypothesis = model(x)
# cost 계산
cost = F.binary_cross_entropy(hypothesis, y)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
if i % 10 == 0 :
prediction = hypothesis >= torch.tensor([0.5])
correct_prediction = prediction == y
accuracy = correct_prediction.sum().item() / len(correct_prediction)
print("epoch : {:d} | Cost : {:5.4f} | accuracy : {:2.2f}%".format(i, cost, accuracy))이제 x의 값이 0보다 작은 값일 때의 x의 값과 0보다 클 때에 대해서 y값을 출력해보자.
print(model(torch.FloatTensor([[0], [-1], [-2], [-3], [-4.5]])))
print(model(torch.FloatTensor([[1], [11], [21], [31], [500]])))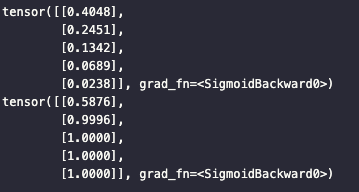
x의 값이 0보다 작을 때는 0.5보다 작은 값을, x의 값이 0보다 클 때는 0.5보다 큰 값을 출력하는 것을 볼 수 있다.
'NLP > 딥러닝을 이용한 자연어 처리 입문' 카테고리의 다른 글
| [NLP] 5-5. 로지스틱 회귀(Logistic Regression) (1) | 2024.01.05 |
|---|---|
| [NLP] 5-4. 자동 미분과 선형 회귀 실습 (0) | 2024.01.04 |
| [NLP] 5-3. 선형 회귀 (1) | 2024.01.04 |
| [NLP] 5-2. 머신 러닝 훑어보기 (1) | 2024.01.03 |
| [NLP] 5-1. 머신 러닝이란 (0) | 2024.01.03 |
