Union-Find 알고리즘
- '합집합 찾기'라는 의미를 가진 알고리즘
- 서로소 집합 알고리즘이라고도 부름
- 여러 개의 노드가 존재할 때 두 개의 노드를 선택해서, 현재 이 두 노드가 서로 같은 그래프에 속하는지 판별하는 알고리즘
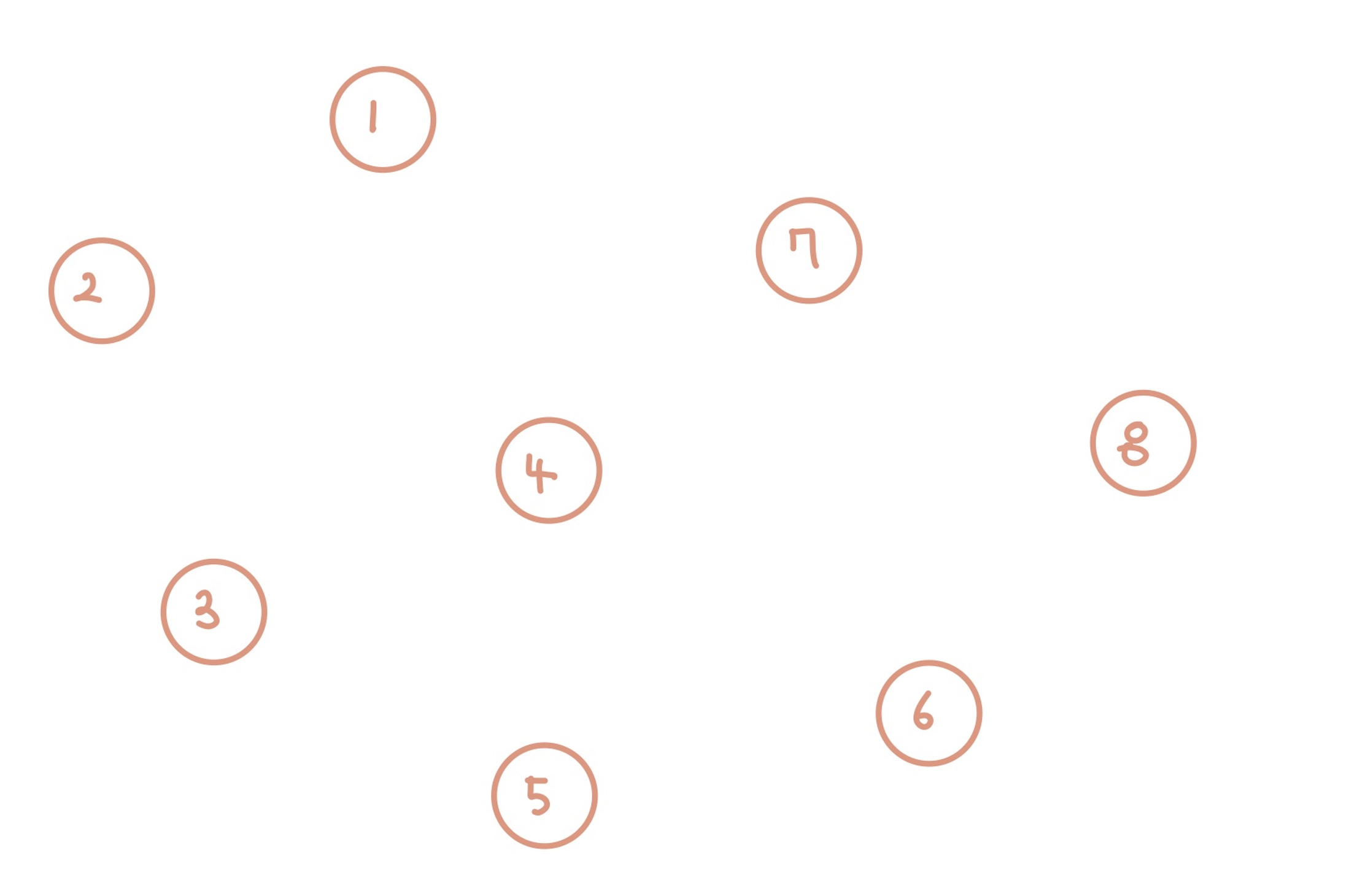
위와 같이 여러 개의 노드가 있다고 가정한다.
이와 같이 모두 연결되지 않고 각자 자기 자신만을 집합의 원소로 가지고 있을 때, 즉 모든 값이 자기 자신을 가리키도록 만든다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
이 때 노드 1과 2가 연결되었다고 가정한다.
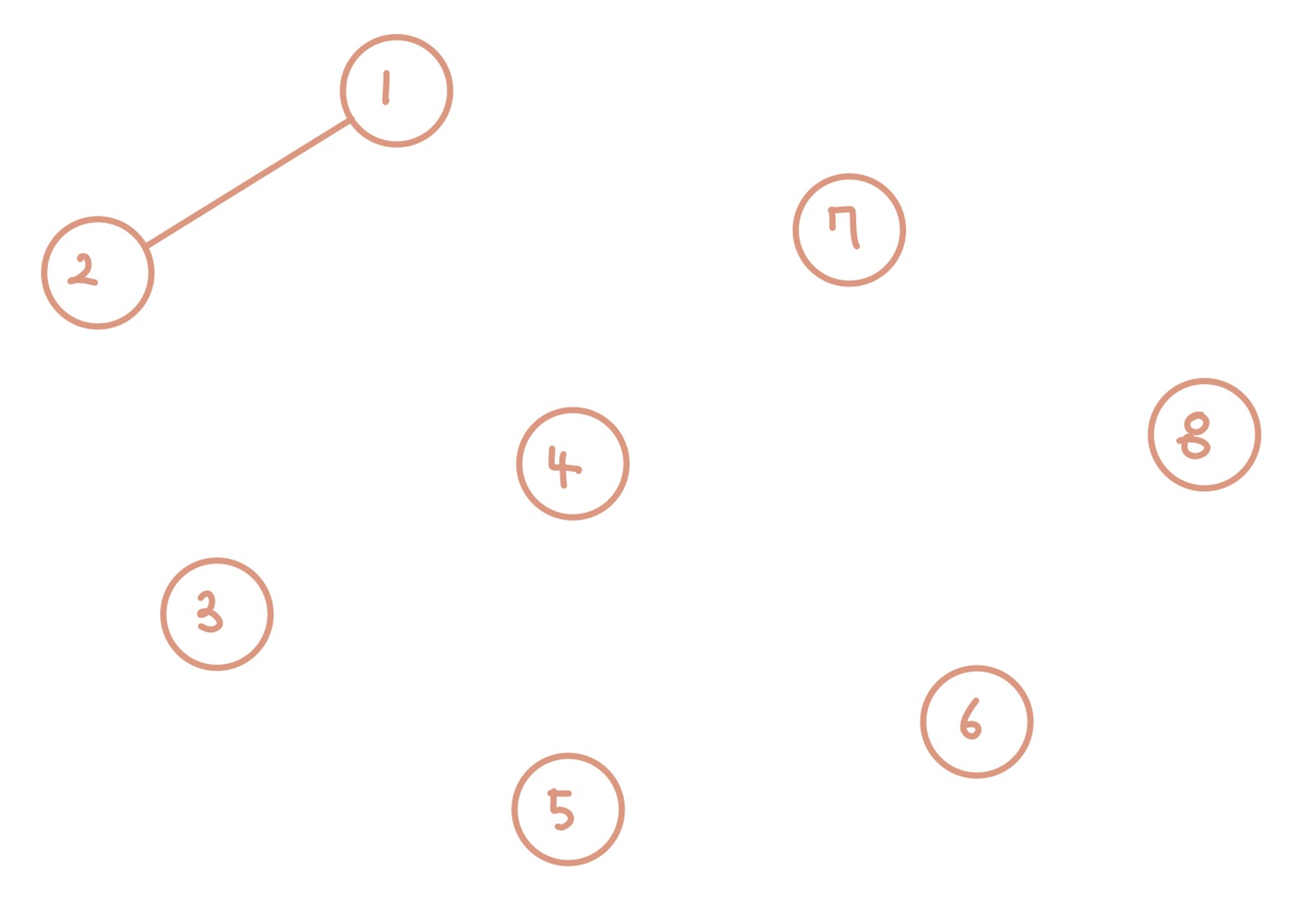
이러한 '연결성'을 우리가 프로그래밍 언어로 어떻게 표현할 수 있을지에 대한 내용이 Union-Find 알고리즘
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 1 | 3 | 4 | 5 | 6 | 7 | 8 |
위 표와 같이 2번째 인덱스의 값에 1이 들어간다.
이렇게 부모를 합칠 때는 일반적으로 더 작은 값 쪽으로 합친다.
이것을 Union(합침)이라고 한다.
만약 2와 3도 연결되었다면?
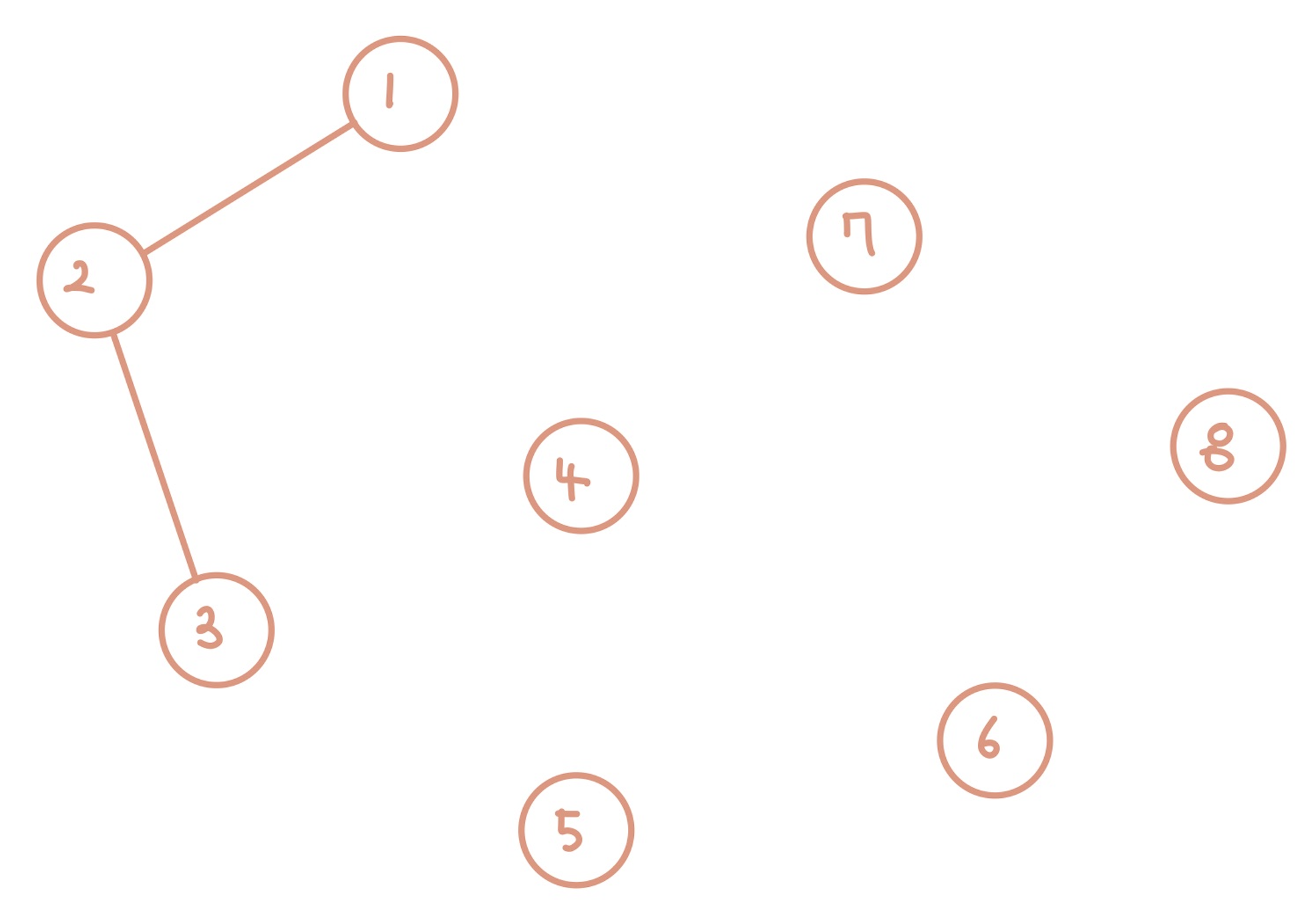
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 1 | 2 | 4 | 5 | 6 | 7 | 8 |
위와 같이 표현된다.
만약 1번 노드와 3번 노드가 연결되었는지 어떻게 파악할 수 있을까?
1번 노드와 3번 노드는 부모가 각각 1과 2로 다르기 때문에 '부모 노드'만 보고는 한 번에 파악할 수 없다.
그렇기 때문에 재귀함수가 사용된다.
3번 노드의 부모를 찾기 위해서는 먼저 3번 노드가 가리키고 있는 2를 찾는다.
그러면 2번 노드의 부모가 1을 가리키고 있으므로 3번 노드의 부모는 1번 노드가 된다는 것을 알 수 있다.
그래서 결과적으로 Union(합침) 연산이 다 수행되고 나면 다음과 같이 표가 구성된다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 1 | 1 | 4 | 5 | 6 | 7 | 8 |
노드 1, 2, 3의 부모가 모두 1이기 때문에 이 세 노드는 모두 같은 그래프에 속한다고 할 수 있다.
Find 알고리즘은 두 개의 노드의 부모 노드를 확인하여 현재 같은 집합에 속하는지 확인하는 알고리즘이다.
이러한 Union-Find 알고리즘은 다른 고급 그래프 알고리즘의 베이스가 된다는 점에서 반드시 익혀야 한다.
Code
def union(x, y) :
x = find(x)
y = find(y)
# 더 작은 루트 노드에 합친다.
if x < y : root[y] = x
else : root[x] = y
def find(x) :
# 루트 노드를 찾을 때까지 재귀 호출
if root[x] != x :
return find(root[x])
return x
SIZE = 8
# 루트 노드 리스트 생성
root = list(range(SIZE + 1))
# 1번 노드와 2번 노드 연결
union(1, 2)
# 2번 노드와 3번 노드 연결
union(2, 3)
print(root) # [0, 1, 1, 1, 4, 5, 6, 7, 8]'Algorithm' 카테고리의 다른 글
| 최장 증가 수열(LIS, Longest Increasing Subsequence) 알고리즘 (0) | 2023.07.16 |
|---|---|
| 크루스칼 알고리즘 (0) | 2023.07.08 |
| 최장 공통 부분 수열 (LCS, Longest Common Subsequence) 알고리즘 (0) | 2023.06.30 |
| Knapsack(배낭 문제) (0) | 2023.05.15 |
| 플로이드-워셜 알고리즘 (0) | 2023.05.08 |
