728x90
크루스칼 알고리즘
- 가장 적은 비용으로 모든 노드를 연결하기 위해 사용하는 알고리즘
- 최소 비용 신장 트리를 만들기 위한 대표적인 알고리즘
-> 여러 개의 도시가 있을 때 각 도시의 도로를 이용해 연결하고자 할 때 비용을 최소한으로 하기 위해 적용되는 알고리즘

핵심 개념
간선을 거리가 짧은 순서대로 그래프에 포함시키면 어떨까?
주의 사항
사이클이 발생하지 않아야 한다.
- 사이클이란 그래프가 서로 연결되어 사이클을 형성하는 경우
- 최소 비용 신장 트리에서는 사이클이 발생하지 않아야 한다.

- 사이클 발생 여부는 Union-Find 알고리즘을 적용하면 된다.
동작 과정
- 모든 간선들을 '거리(비용)' 기준으로 먼저 오름차순 정렬 수행
- 정렬된 순서에 맞게 그래프에 포함시킨다.
- 포함시키기 전에 사이클 테이블을 확인한다.
- 사이클을 형성하는 경우 간선을 포함하지 않는다.
[Step 0] 초기 상태

[Step 1] 첫 번째 간선을 선택
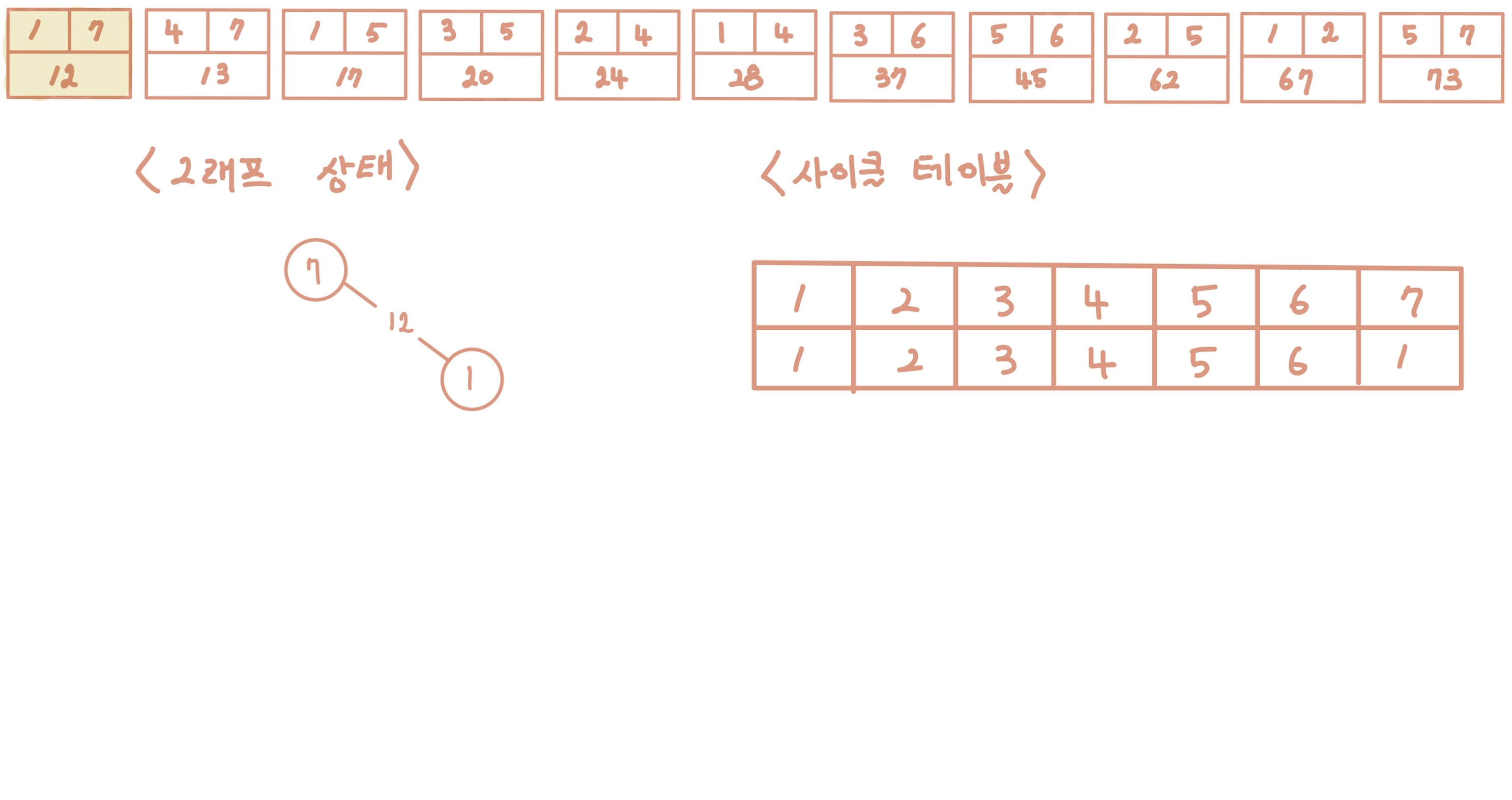
[Step 2] 두 번째 간선을 선택
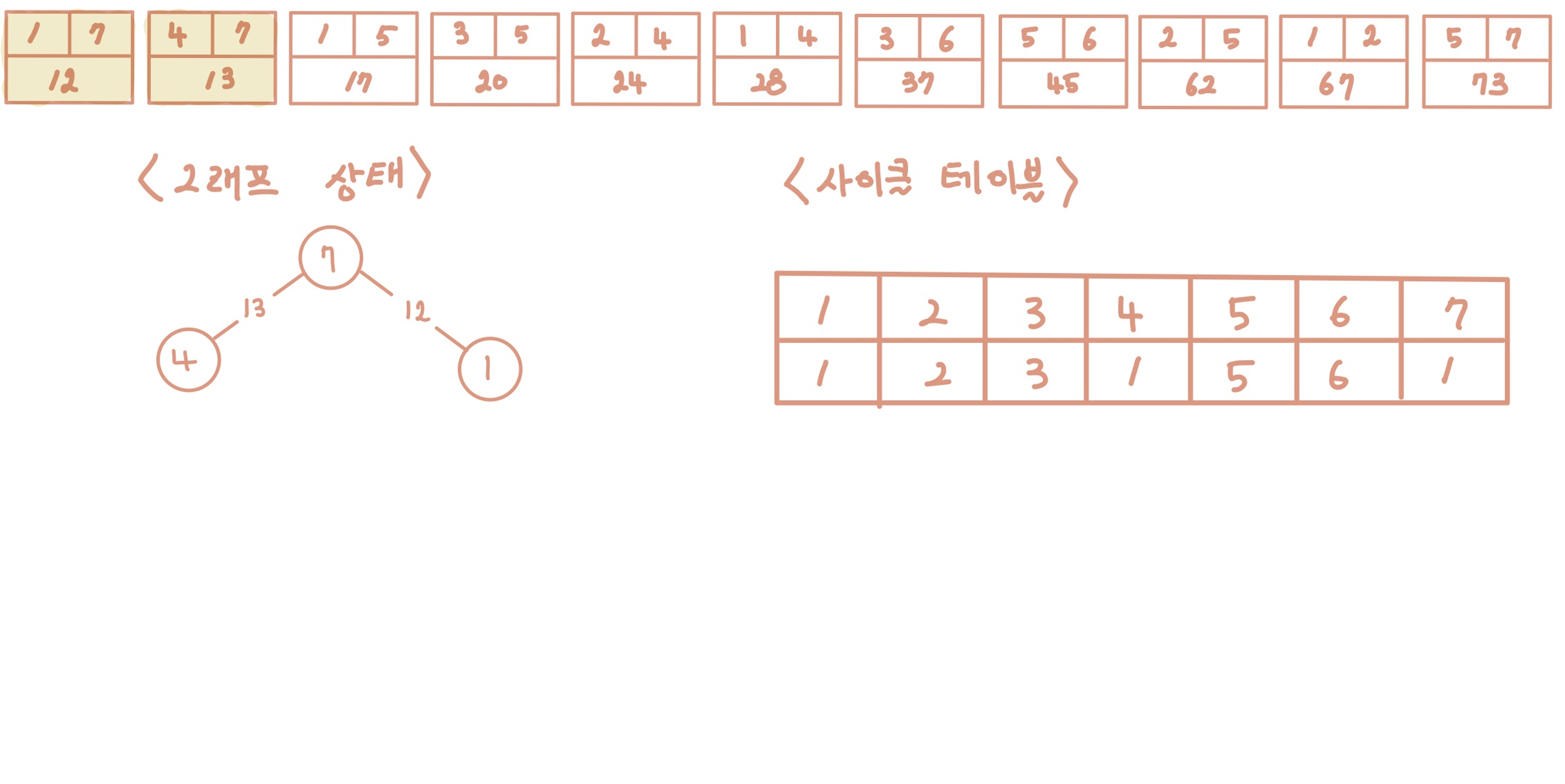
[Step 3] 세 번째 간선을 선택

[Step 4] 네 번째 간선을 선택
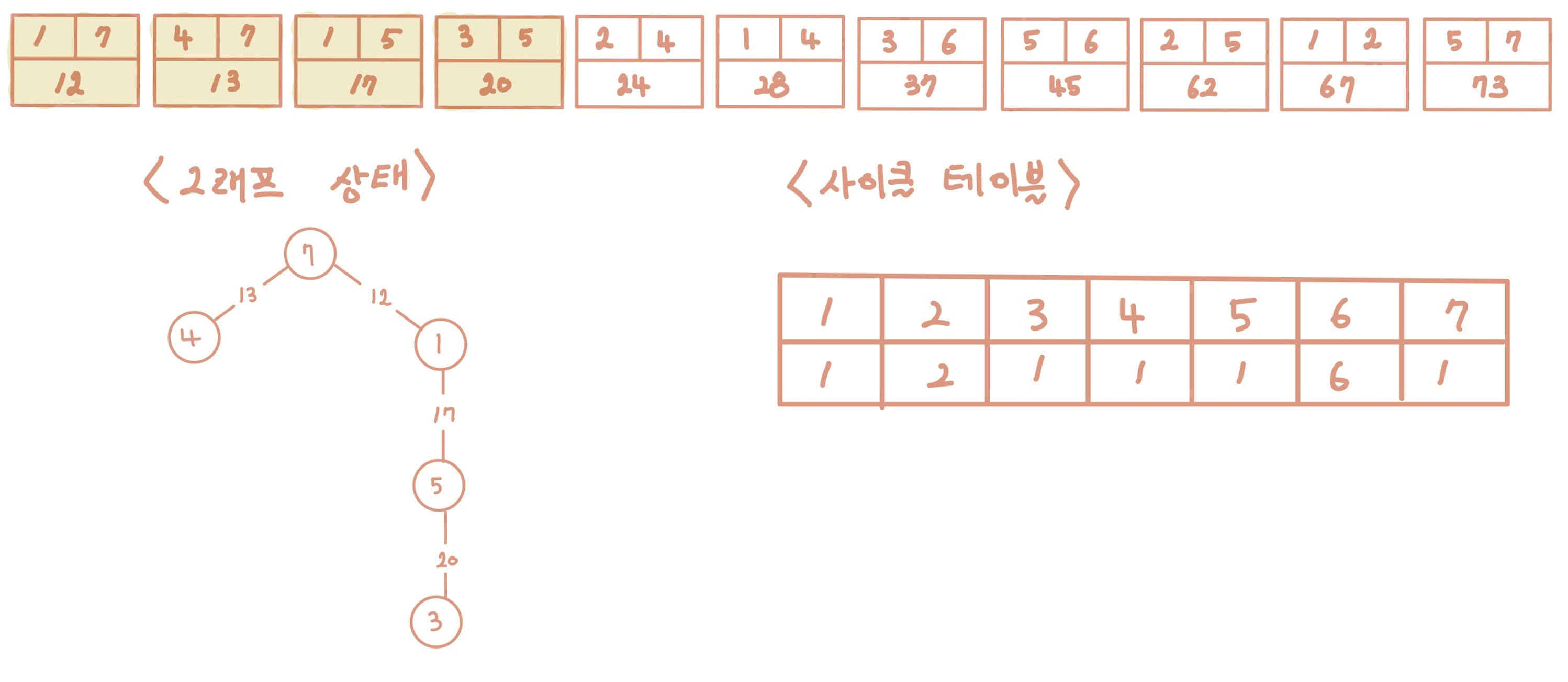
[Step 5] 다섯 번째 간선을 선택

[Step 6] 여섯 번째 간선을 선택
-> 1과 4가 이미 연결되어 있으므로(사이클 테이블의 값이 동일하므로) 무시하고 넘어간다.
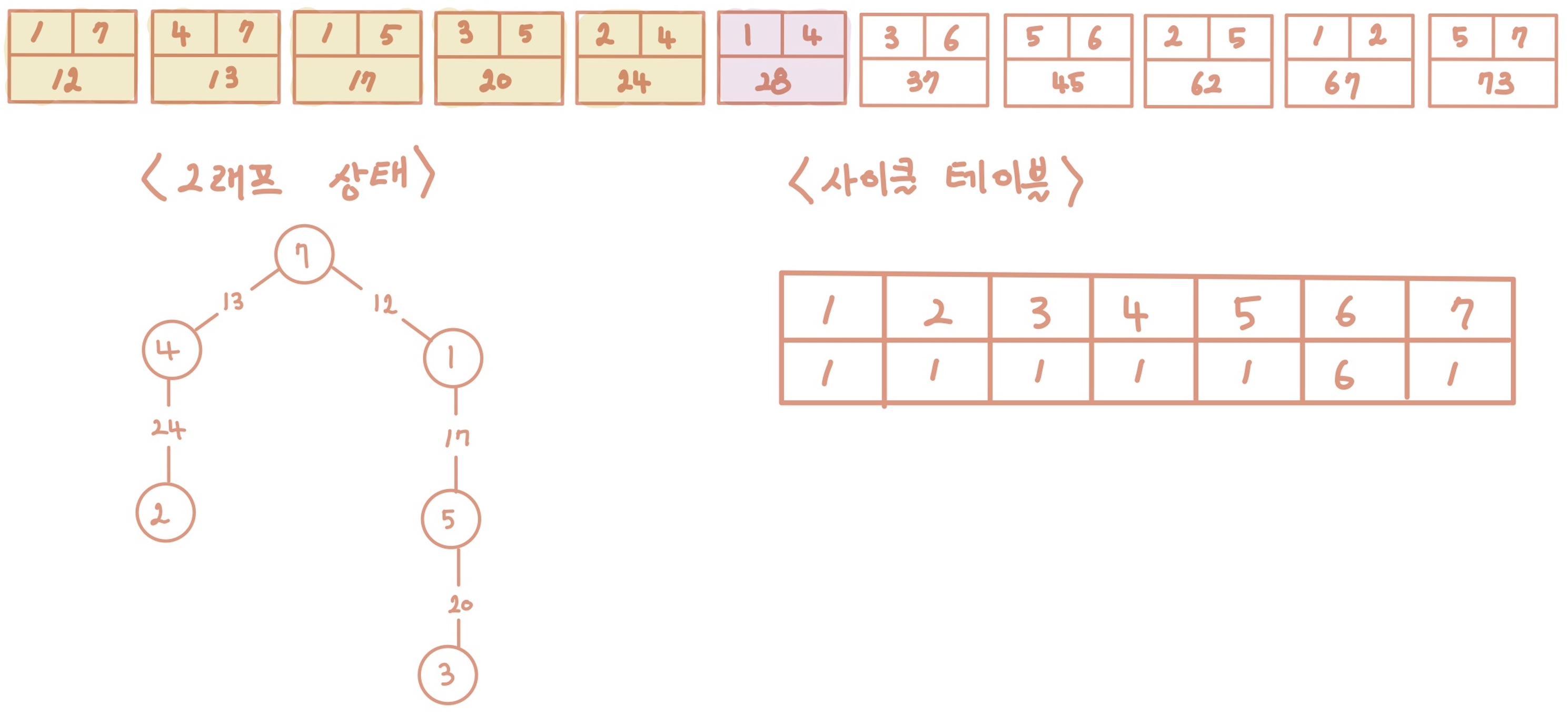
[Step 7] 일곱 번째 간선을 선택
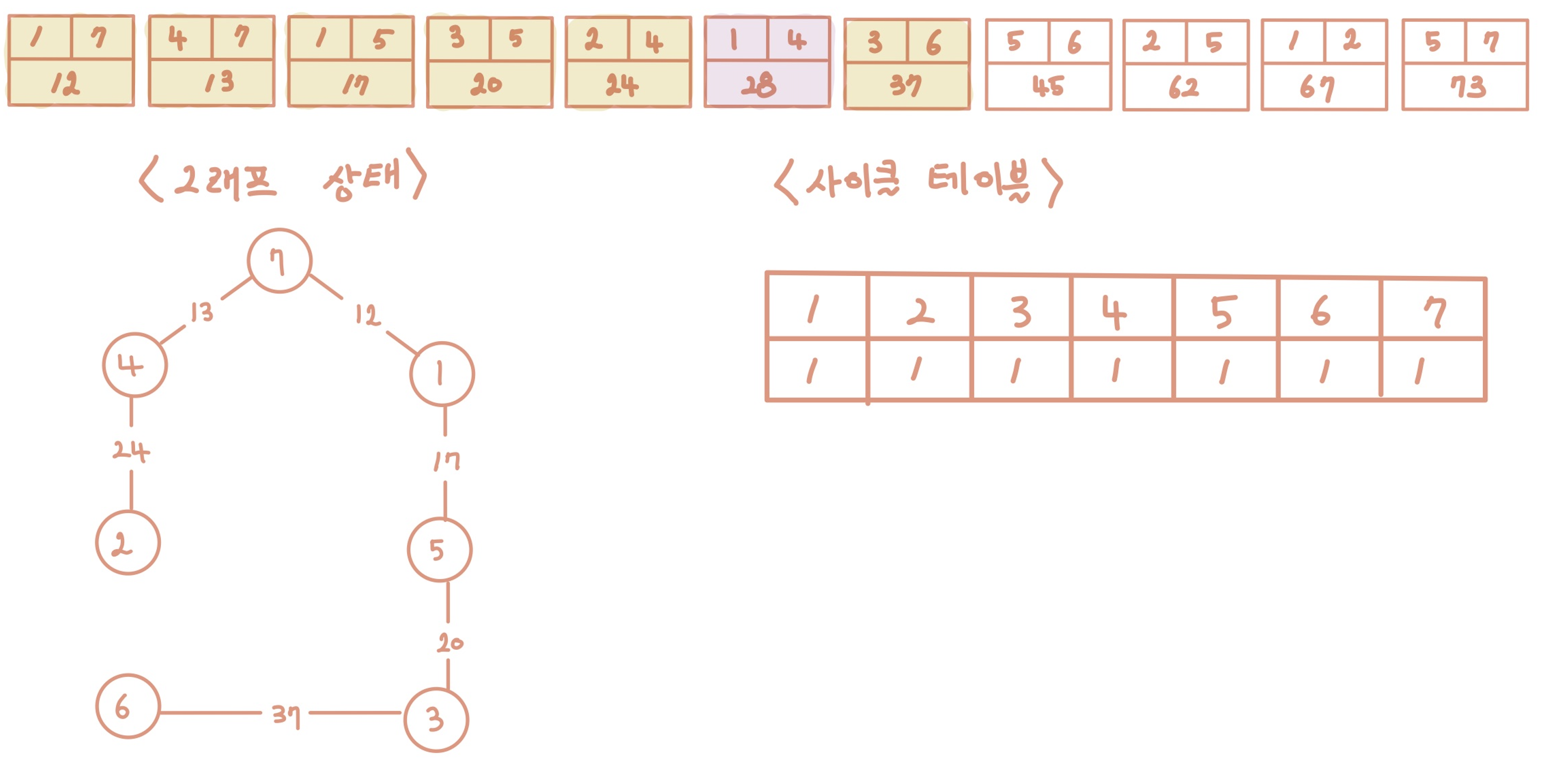
[Step 8] 사이클 테이블의 모든 값이 1이 되면서 최소 비용 신장트리가 만들어진다.
-> 나머지 남은 간선 4개는 모두 스킵 처리되면서 결과적으로 다음과 같이 완성

Code
def union(x, y) :
x = find(x)
y = find(y)
# 더 작은 루트 노드에 합친다.
if x < y : root[y] = x
else : root[x] = y
def find(x) :
# 루트 노드를 찾을 때까지 재귀 호출
if root[x] != x :
return find(root[x])
return x
SIZE = 7
costs = [(1, 7, 12), (1, 4, 28), (1, 2, 67), (1, 5, 17), (2, 4, 24), (2, 5, 62), (3, 5, 20), (3, 6, 37), (4, 7, 13), (5, 6, 45), (5, 7, 73)]
# 모든 간선들을 '거리(비용)' 기준으로 오름차순 정렬 수행
costs.sort(key = lambda x : x[2])
distance = 0
# 루트 노드 리스트 생성
root = list(range(SIZE + 1))
for start, end, cost in costs :
# 사이클 테이블 확인
if find(start) != find(end) :
distance += cost
# start 노드와 end 노드 연결
union(start, end)
print(distance) # 123
print(root) # [0, 1, 1, 1, 1, 1, 1, 1]728x90
'Algorithm' 카테고리의 다른 글
| 비트마스크(BitMask) (0) | 2023.11.27 |
|---|---|
| 최장 증가 수열(LIS, Longest Increasing Subsequence) 알고리즘 (0) | 2023.07.16 |
| Union-Find 알고리즘 (0) | 2023.07.08 |
| 최장 공통 부분 수열 (LCS, Longest Common Subsequence) 알고리즘 (0) | 2023.06.30 |
| Knapsack(배낭 문제) (0) | 2023.05.15 |
