728x90
반응형
https://www.acmicpc.net/problem/5639
5639번: 이진 검색 트리
트리를 전위 순회한 결과가 주어진다. 노드에 들어있는 키의 값은 106보다 작은 양의 정수이다. 모든 값은 한 줄에 하나씩 주어지며, 노드의 수는 10,000개 이하이다. 같은 키를 가지는 노드는 없다
www.acmicpc.net
문제
이진 검색 트리는 다음과 같은 세 가지 조건을 만족하는 이진 트리이다.
- 노드의 왼쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 작다.
- 노드의 오른쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 크다.
- 왼쪽, 오른쪽 서브트리도 이진 검색 트리이다.
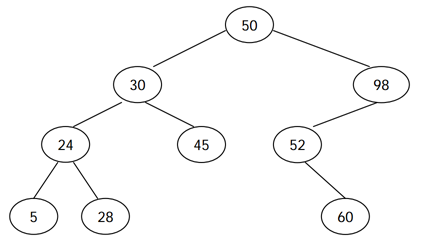
전위 순회 (루트-왼쪽-오른쪽)은 루트를 방문하고, 왼쪽 서브트리, 오른쪽 서브 트리를 순서대로 방문하면서 노드의 키를 출력한다. 후위 순회 (왼쪽-오른쪽-루트)는 왼쪽 서브트리, 오른쪽 서브트리, 루트 노드 순서대로 키를 출력한다. 예를 들어, 위의 이진 검색 트리의 전위 순회 결과는 50 30 24 5 28 45 98 52 60 이고, 후위 순회 결과는 5 28 24 45 30 60 52 98 50 이다.
이진 검색 트리를 전위 순회한 결과가 주어졌을 때, 이 트리를 후위 순회한 결과를 구하는 프로그램을 작성하시오.
입력
트리를 전위 순회한 결과가 주어진다. 노드에 들어있는 키의 값은 106보다 작은 양의 정수이다. 모든 값은 한 줄에 하나씩 주어지며, 노드의 수는 10,000개 이하이다. 같은 키를 가지는 노드는 없다.
출력
입력으로 주어진 이진 검색 트리를 후위 순회한 결과를 한 줄에 하나씩 출력한다.
풀이


Code(시간 초과) - 리스트
import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
def binary_tree(arr) :
# 1-1. 종료 조건 설정
if len(arr) == 1 :
print(arr[0])
return
# 1-2. 오른쪽 서브 노드 인덱스 찾기
i = 1
while i < len(arr) and arr[0] > arr[i] : i += 1
# 1-3. 분할정복 1 : 왼쪽 서브 노드 부분 이진 탐색 트리 실행
left = arr[1:i]
if left : binary_tree(left)
# 1-4. 분할정복 2 : 오른쪽 서브 노드 부분 이진 탐색 트리 실행
right = arr[i:]
if right : binary_tree(right)
# 1-5. 루트 노트 출력
print(arr[0])
# 2. 전위 순회 결과 입력받기
array = []
while True :
try :
array.append(int(input()))
except :
break
# 3. 이진 탐색 트리 실행
binary_tree(array)Code - 인덱스
import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
# 1. 이진 탐색 트리 함수 선언
def binary_tree(start, end) :
# 1-1. 종료 조건 설정
if start > end : return
# 1-2. 오른쪽 서브 노드 인덱스 찾기
mid = start + 1
while mid < len(array) and array[start] > array[mid] : mid += 1
# 1-3. 분할정복 1 : 왼쪽 서브 노드 부분 이진 탐색 트리 실행
binary_tree(start+1, mid-1)
# 1-4. 분할정복 2 : 오른쪽 서브 노드 부분 이진 탐색 트리 실행
binary_tree(mid, end)
# 1-5. 루트 노트 출력
print(array[start])
# 2. 전위 순회 결과 입력받기
array = []
while True :
try :
array.append(int(input()))
except :
break
# 3. 이진 탐색 트리 실행
binary_tree(0, len(array) - 1)728x90
반응형
'Coding Test > Baekjoon' 카테고리의 다른 글
| [Python/BOJ] 12099. 점심메뉴 (0) | 2023.08.12 |
|---|---|
| [Python/BOJ] 18869. 멀티버스 Ⅱ (0) | 2023.08.12 |
| [Python/BOJ] 17394. 핑거 스냅 (0) | 2023.08.11 |
| [Python/BOJ] 10819. 차이를 최대로 (0) | 2023.08.11 |
| [Python/BOJ] 1699. 제곱수의 합 (0) | 2023.08.11 |
